Призма. Формули і властивості призми

Визначення призми

• Призма — це багатогранна об’ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться у двох паралельних площинах, а інші грані (бічні грані) — паралелограми, що мають спільні сторони з цими багатокутниками.

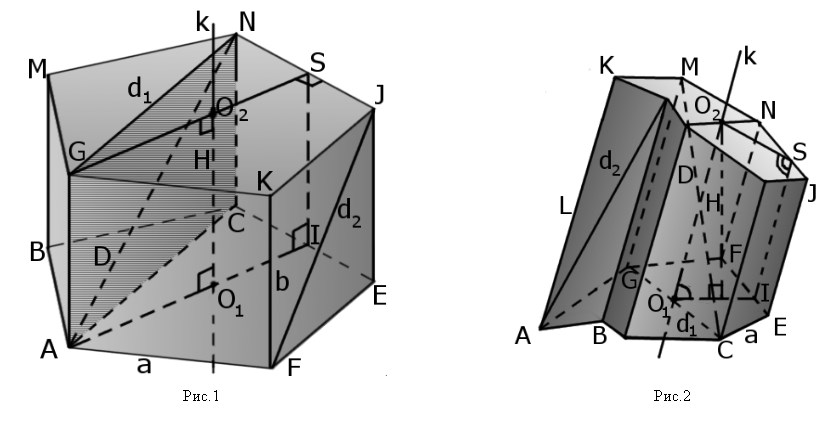
• Основи призми — дві грані, які є рівними паралельними плоскими багатокутниками (ABCEF, GMNJK).
• Бічні грані призми — всі інші грані за винятком основ.
• Бічна поверхня призми — сукупність всіх бічних граней призми.
• Поверхня призми — це сукупність поверхонь двох основ і бічної поверхні.
• Бічне ребро призми — спільна сторона двох бічних граней.
• Висота — це перпендикуляр, який з’єднує дві основи призми під прямим кутом.
• Діагональ основи призми — це відрізок, що з’єднує дві не сусідні вершини, що належать цій же основі.
• Діагональ бічної грані призми — це відрізок, що з’єднує дві протилежні вершини, що лежать на одній бічній грані однак належать до різних основ.
• Діагональ призми (AN) — це відрізок, що з’єднує дві вершини, що лежать на різних основах але не лежать на одній бічній стороні.
• Діагональний перетин — це перетин призми площиною, що проходить через діагональ основи призми і бічне ребро. Трикутна призма (в основі призми, трикутники) не має діагональних перерізів.
• Перпендикулярний переріз — це перетин призми площиною, що перетинає бічні ребра призми під прямим кутом.
• Пряма призма — це призма, в якій всі бічні грані перпендикулярні до основи. Висота дорівнює довжині бічного ребра.
• Похила призма — це призма, у якої бічні грані не перпендикулярні до основи.
• Правильна призма — це призма, в якій основи є правильними многокутниками. Правильна призма може бути як прямою, так і похилою.
• Усічена призма — це призма, в якій дві основи не паралельні (мал. 2). Усічена призма може бути як пряма, так похила.

Читайте також: Правильна трикутна призма: характеристики, формули, розгортки

Призма формули

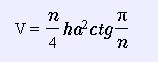
Площа поверхні призми

Формула. Площа бічної поверхні призми через периметр основи і висоту:S_b = P·h

Формула.Площа поверхні призми через площу основи, периметр основи і висоту:S = 2S_осн + P·h

Формула.Площа поверхні призми через висоту (h), довжину сторони (a) і кількість сторін (n):

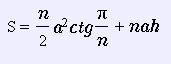
Формула. Площа правильної трикутної призми складається з двох площ основ і трьох площ бічних граней (мал. нижче) Sпризмы= 2·Sосн+ 3·Sбіч.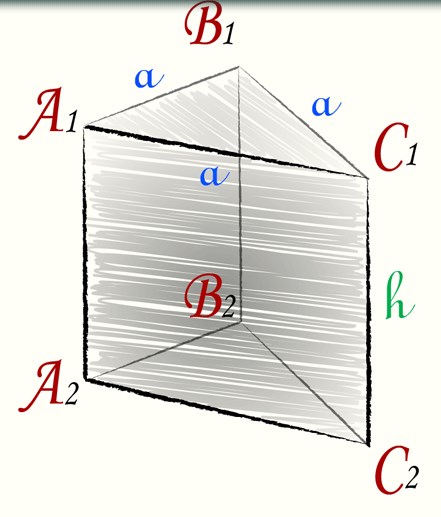

Підставимо сюди формулу площі прямокутника і формулу площі рівностороннього трикутника і отримаємо:

Основні властивості призми

• Основи призми — рівні многокутники.
• Бічні грані призми — паралелограми.
• Бічні ребра призми паралельні і рівні між собою.
• Перпендикулярний переріз перпендикулярній всім бічним ребрам і бічним граням.
• Висота прямої призми дорівнює довжині бічного ребра.
• Висота похилої призми завжди менше довжини ребра.
• У прямій призмі гранями можуть бути прямими або квадратами.